[Activation] 1. Activation Function

활성화 함수(Activation Function)란?

• 입력 신호의 총합을 출력 신호로 변환하는 함수다. 이를 통해 이전 층(layer)의 결과값을 변환하여 다른 층의 뉴런으로 전달할 수 있다. 대표적으로 Sigmoid, Softmax, ReLU 등이 있다.
• Neural Network(NN) 을 살펴봤던 포스트에서 공부했듯, 인공 신경망은 인간 두뇌 활동을 모방하기 위해 뉴런의 구조를 참고했다. 최초의 인공 신경망인 퍼셉트론은 계단 함수(Step function)를 활성화 함수로 사용했다.
• 그러나 계단 함수를 활성화 함수로 사용하면, 인공 신경망의 학습이 제대로 이루어지기 어려웠다.
  • 인간은 하나의 분야를 탐구하면서 지속적으로 학습하는데, 계단 함수는 이러한 인간 학습의 연속성을 표현할 수 없었기 때문이다.
  • 또한 인공 신경망은 학습을 위하여 gradient 기반의 경사하강법을 이용하는데, 이는 연쇄법칙을 활용한 미분을 토대로 계산된다. 그러나 계단 함수는 미분 불가능한 함수이기 때문에 경사하강법을 통한 역전파(back propagation)로 학습이 되지 않는다.
• 따라서 활성화 함수는 값을 전달할 때 연속성을 부여할 수 있는, 즉 미분 가능한 함수를 사용한다. 또한 활성화 함수는 비선형 함수를 사용한다.
• 그 이유의 첫번째는 Neural Network 의 표현력을 높이기 위해서이다.
  • 현실 세계의 대부분 문제는 비선형 문제이기 때문에, 비선형 활성화 함수를 사용하면 모델이 문제를 더 효과적으로 풀 수 있게 된다. 또한, 다양한 비선형 활성 함수를 조합하여 사용함으로써 그 효과는 배가 될 수 있다.
• 두번째는 선형 함수로는 독립변수와 종속변수 사이의 다양한 관계를 파악하기 어렵다.
  • Neural Network 는 성능을 위하여 hidden layer 를 여러 층으로 쌓는데, 이 hidden layer 도 affine transformation 으로서 선형 함수다.
  • 선형 함수가 여러 개 쌓은 결과는 결국 선형 함수다. 따라서 활성화 함수로 선형 함수를 사용하게 되면, 여러 층을 통과하는 결과값을 단 하나의 층으로도 표현할 수 있게 되면서 layer 를 깊게 쌓는 의미가 희석되는 것이다.

Affine Transformation

• 수식적으로 살펴보면, 선형 함수는 아래와 같이 나타낼 수 있다.

  \[f(x) = \mathbf{W}\mathbf{x} + \mathbf{b}\]

• 이는 입력에 대해 Linear Transformation($\mathbf{W}$) 과 Translation term($\mathbf{b}$) 이 합쳐진 Affine Transformation 이다.

  Affine Transformation.
  출처: https://towardsdatascience.com/understanding-transformations-in-computer-vision-b001f49a9e61

• 위 gif 영상을 보면, affine transformation 에 의해 격자 전체가 함께 변화함을 확인할 수 있다.

• 이처럼 Affine transformation 은 어떤 공간(space)을 변형시키는 것으로 생각할 수 있다. 이러한 변형으로 우리는 풀지 못했던 문제를 풀 수도 있다.

  

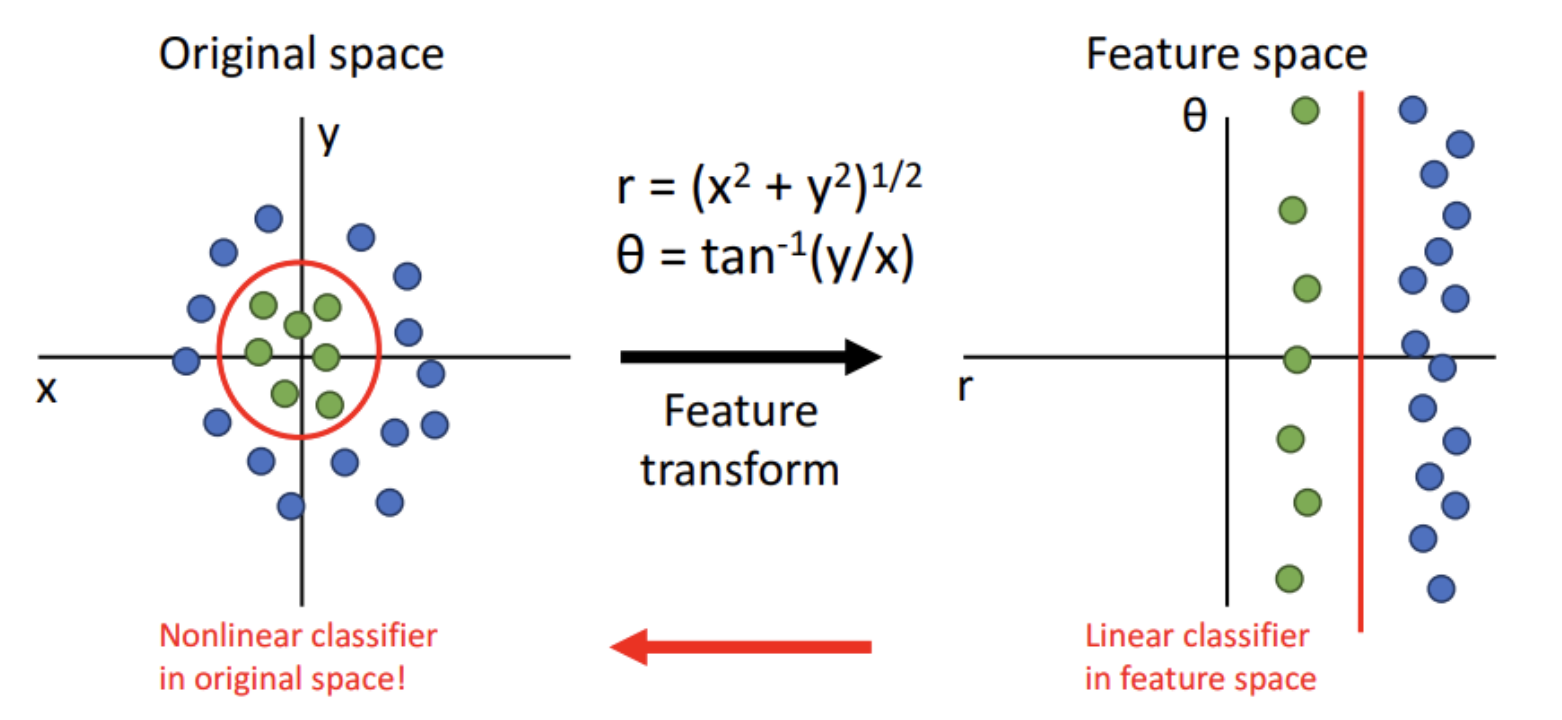
• 위 그림을 보면 공간의 변형으로 기존에 구분하지 못했던 점들을 직선으로 구분할 수 있다. 물론 affine transformation 만으로 위와 같은 구분은 불가능하다.
• 이러한 공간 변형을 딥러닝에 비추어 생각해보자.

• Neural Network 는 위에서 봤듯 여러 hidden layer 를 쌓은 형태다. 이 2 개의 hidden layer 를 가진 모델의 출력은 아래와 같이 나타낼 수 있다.

  \[\begin{aligned} \mathbf{H} & = \mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}, \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}. \end{aligned}\]

• 이는 위에서 본 Affine transformation 식의 형태와 같으며 이를 통해 공간이 변형(space warping)된다.

  

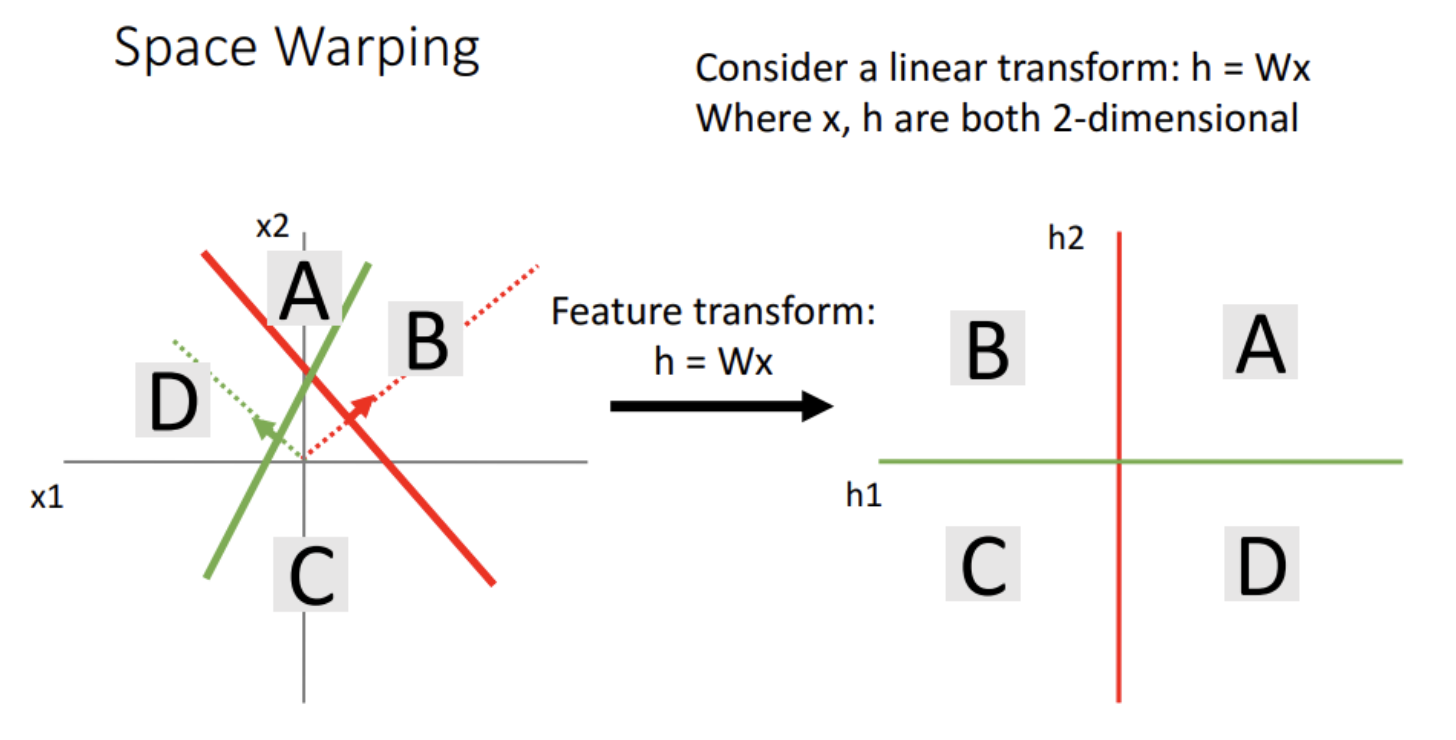
• bias 또한 parameter 로서 $w_0$ 와 같은 형태로 생각하면, $\mathbf{H} = \mathbf{XW}$ 로 생각할 수 있다.
• 이렇게 hidden layer 를 통과하면 공간이 변형되고, 위 그림처럼 A, B, C, D 를 직선으로 쉽게 구분할 수 있다.
• 이처럼 neural network 는 Affine Transformation 이 여러 번 가해진 형태다. 그러나 이러한 여러 개의 선형 함수를 쌓는 것은 결국 한 개의 선형 함수를 사용하는 것과 같다고 볼 수 있다.
• 그렇게 되면, 즉 비선형 함수인 활성화 함수가 없다면, 여러 개의 hidden layer 를 가진 neural network 와 1 개의 hidden layer 를 가진 neural network 의 차이가 거의 없어지게 되는 것이다.
• 따라서 모델 입장에서 봤을 때, 이는 모델의 표현력과 성능을 현격히 저하시키고 층을 깊게 쌓는 의미를 퇴색시킨다.

Non-Linearity

• 비선형(non-linearity)의 뜻을 알기 위해서는 우선 선형(linearity)가 무엇인지 알아야 한다.
• 어떤 모델이 선형적(linearity)라고 한다면, 그 모델은 변수 $x_1, x_2, … , x_n$ 과 가중치 $w_1, w_2, … , w_n$ 를 가지고 $y = w_1 * x_1 + w_2 * x_2 + … + w_n * x_n$ 으로 표현할 수 있으며, 가산성(Additreivityly)과 동차성(Homogeneity)을 만족해야 한다.
  • 가산성 : 임의의 수 $x, y$ 에 대해 $f(x+y) = f(x) + f(y)$ 가 성립한다.
  • 등차성 : 임의의 수 $x, \alpha$ 에 대해 $f(\alpha x) = \alpha f(x)$ 가 성립한다.
• 이를 만족하지 못하는 모델을 비선형 관계에 있는 모델이라고 한다. 딥러닝에서 이런 비선형 관계는 활성화 함수를 통해 표현할 수 있다.
• 우리는 데이터에 대하여 Classification 또는 Regression 등을 할 때, 데이터의 분포에 맞게 boundary 를 잘 그려줄 수 있다면 좋은 성능을 가진 모델링을 했다고 할 수 있다.
• 데이터의 복잡도가 높아지고 차원이 높아지게 되면 데이터의 분포는 단순히 선형 형태가 아닌 비선형 형태를 가지게 된다. 이러한 데이터 분포를 가지는 경우 단순히 1 차식의 Linear 한 형태로는 데이터를 표현할 수 없기 때문에 Non-Linearity 가 중요하게 된다.

Non-linear Activation function 의 필요성

• 앞서 deep neural network 의 여러 hidden layer 는 Affine transformation 이라는 것을 살펴봤다.

• 위에서 본 것처럼 이는 현실세계 데이터의 복잡한 문제를 풀기에는 적합하지 않다. 아래 그림을 보자.

  

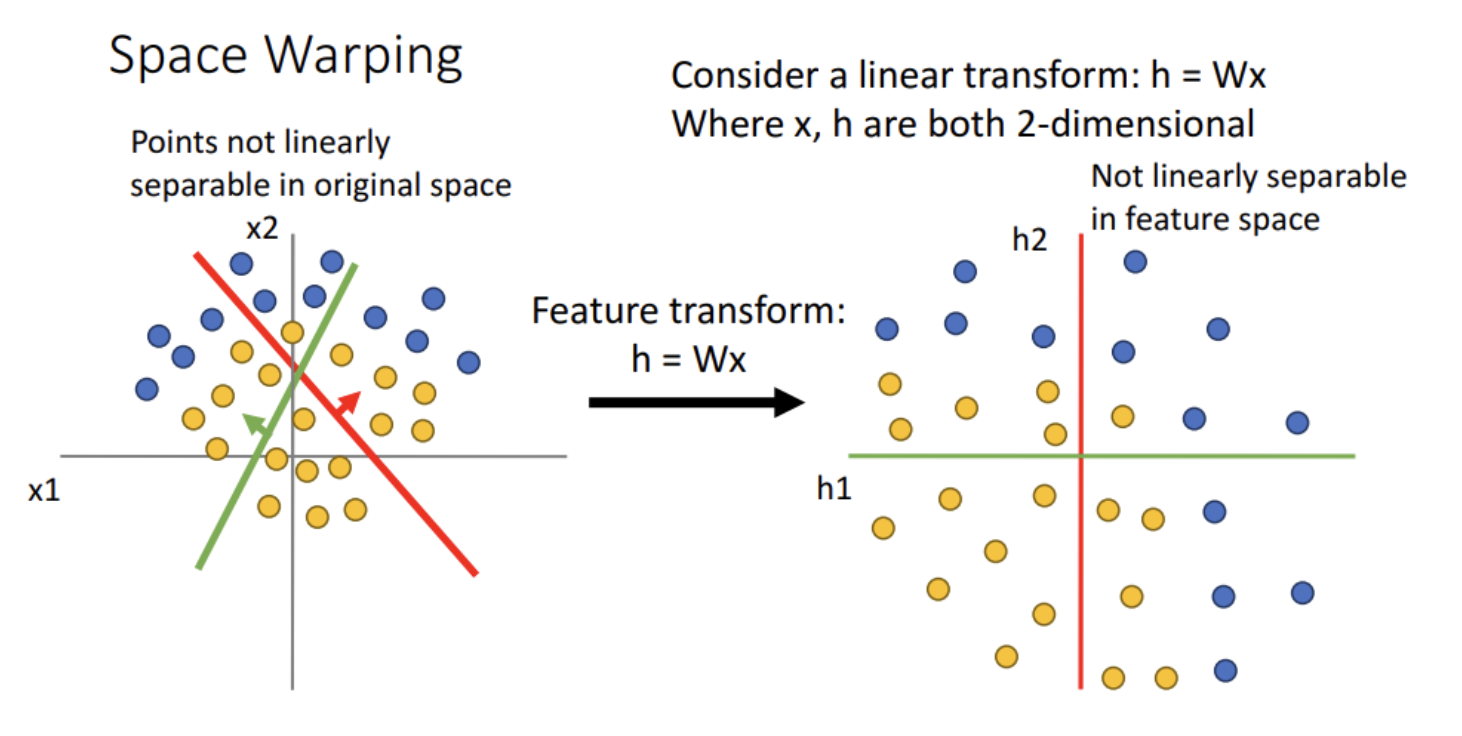
• 기존의 방법대로 가중치를 통해 공간을 변형하더라도, 노랑점과 파랑점은 구분할 수가 없다. 즉 선형 변환만으로는 부족한 상황이다.

• 이 때, 각 축인 h1, h2 에서 0 보다 작은 성분들을 0 으로 변환시켜주는 함수를 이용한다면 어떻게 될까?

  

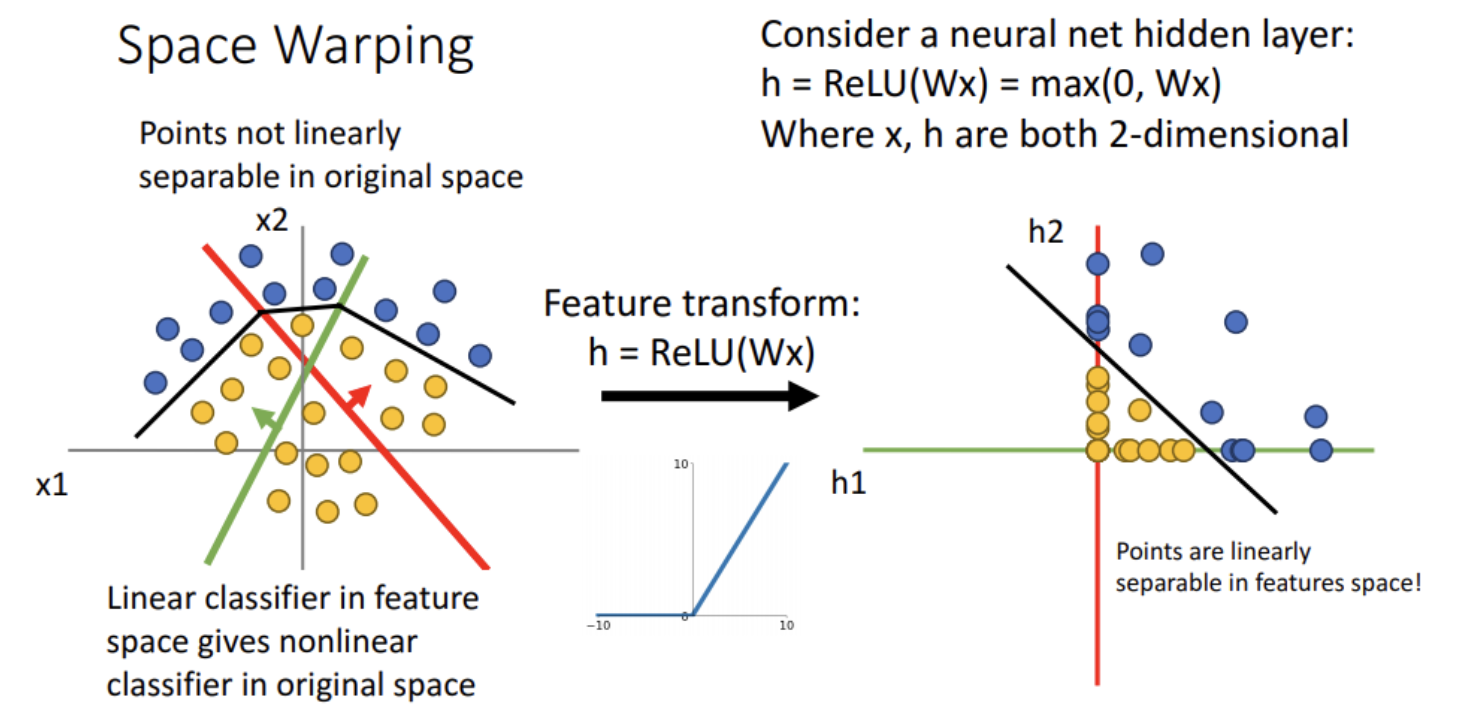
• 위 그림과 같이 직선 하나로 점을 분리할 수 있게 된다.
• 이후 포스트에서 다루겠지만, 0 보다 작은 성분들을 0 으로 변환시켜주는 함수가 바로 활성화 함수 중 오늘날 가장 많이 쓰이는 ReLU 다.
• 이처럼 활성화 함수는 기존 Affine Translation 에 비해서 공간을 더 복잡하게 변형한다. 이를 통해 표현하지 못했던 복잡한 경계도 표현할 수 있다. 그리고 복잡한 경계를 표현할 수 있다면, 결국 더 많고 복잡한 문제들을 해결할 수 있게 될 것이다.

• 아래 gif 영상은 활성화 함수 중 하나인 Tanh 함수가 적용되었을 때의 공간 변형을 나타낸 것이다.

  

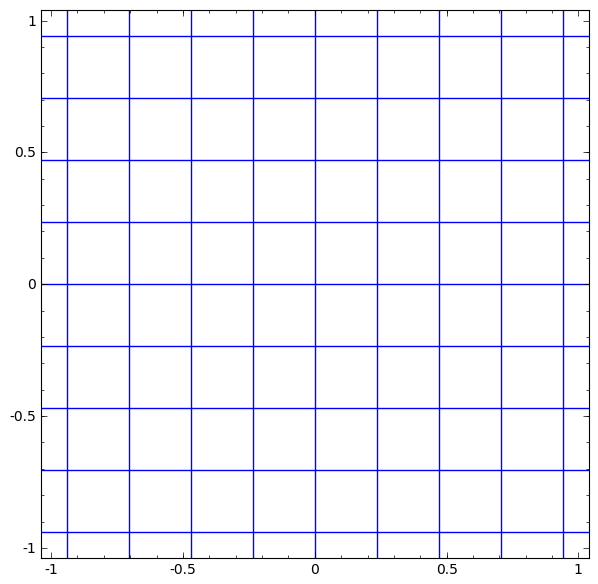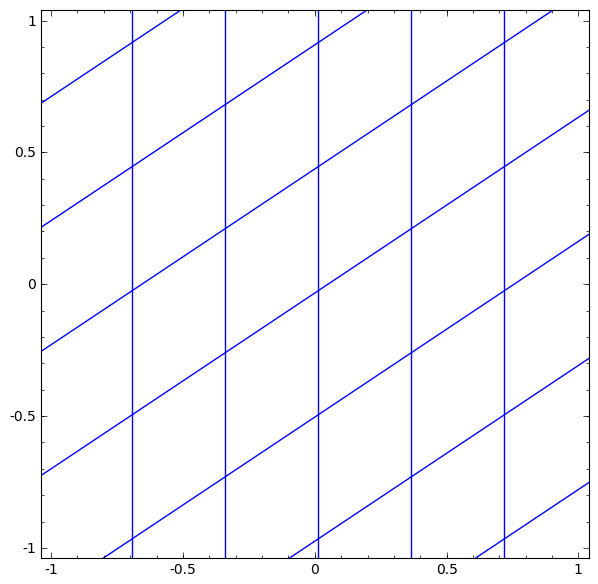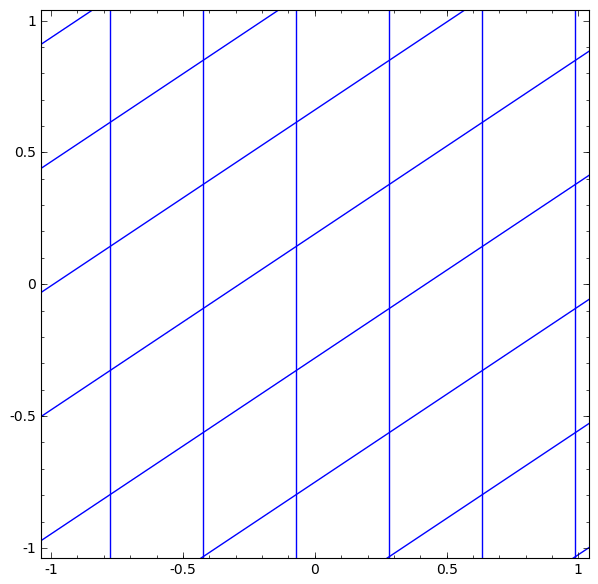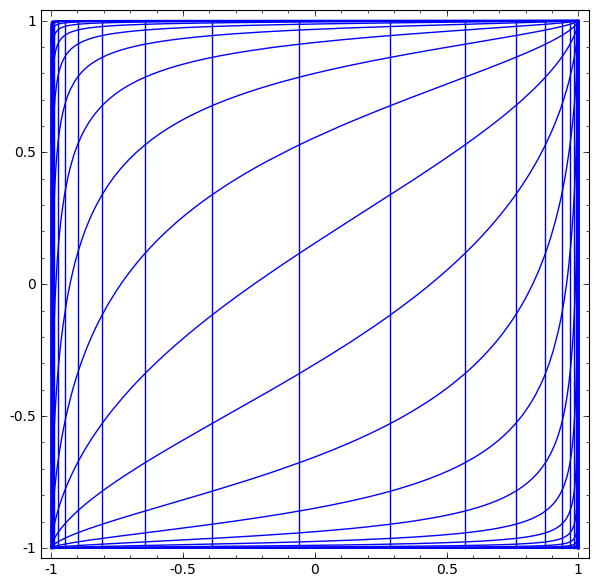
• 선형 변환과 translation 변환 이후 좌표 축이 급격하게 왜곡되는 때가 tanh 가 적용되는 때이다.
• 정리하면, 활성화 함수는 모델에 비선형성을 추가하여 모델의 표현력과 성능을 향상시켜 준다. 또한 layer 를 deep 하게 쌓을수록 단순 선형 변환이 아닌 더 복잡한 결정 경계를 나눌 수 있게 해주는 출발점이다.
  • 이러한 활성화 함수는 gradient 기반의 경사하강법을 통해 최적의 값을 찾아갈 수 있도록 미분 가능한 함수이다.
  • 또한 비선형 함수를 이용한다.

bias

• bias 또한 neural network 에서 최적의 값을 찾는 parameter 중 하나로 학습 과정에서 업데이트 되고 activation function 의 입력값이 된다.
• 이러한 bias 도 앞으로 다룰 각 activation function 의 문제점 등을 생각해볼 때 이 의미가 무엇이고 왜 bias 가 있는 것인지를 알면 좋다.
• 기하학적으로 생각해 보면, bias 는 모델이 데이터에 잘 fitting 하게 하기 위하여 평행 이동하는 역할을 한다.
  • affine transformation 에서 weight term 은 linear transformation 으로서 공간을 skew 혹은 rotate 한다.
  • bias term 은 이를 평행하게 이동시키는 translation term 이다.

• 데이터를 2 차원으로 표현했을 때, 모든 데이터가 원점을 기준으로 분포해 있지는 않다. bias 를 이용하여 모델이 평면 상에서 이동할 수 있도록 하고, 이 bias 또한 학습한다.

  

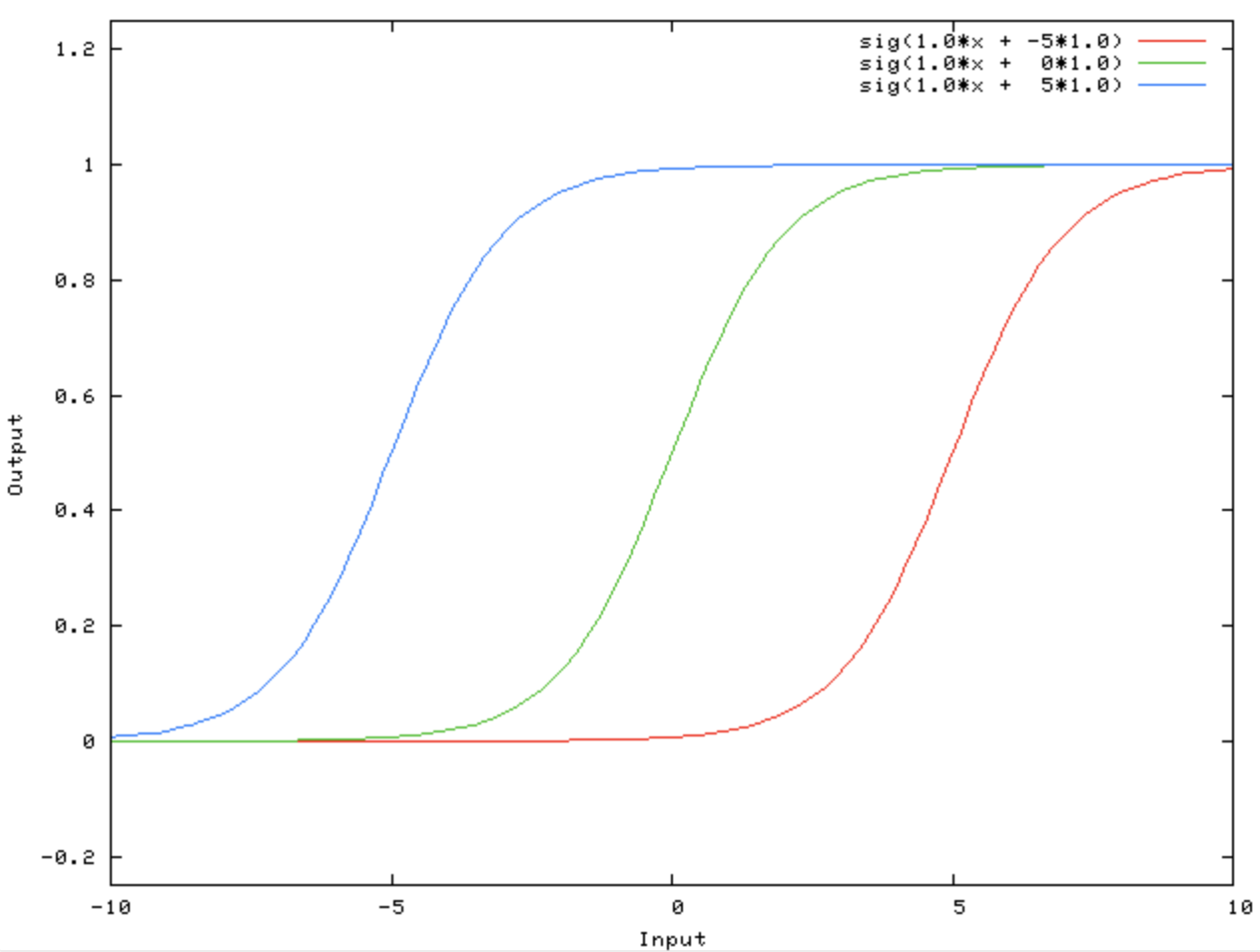
• 위 그림처럼 bias 는 활성화 함수가 왼쪽 혹은 오른쪽으로 이동하게 한다.
• weight 는 활성화 함수의 가파른 정도, 즉 기울기를 조절하는 반면, bias 는 활성화 함수를 움직임으로써 데이터에 더 잘 fitting 하도록 한다.

Acitvation Function 의 종류와 연구방향

• 앞으로 Activation 카테고리에서는 아래의 그림과 같은 다양한 활성화 함수의 종류를 다루는 포스트를 게재할 것이다.

  

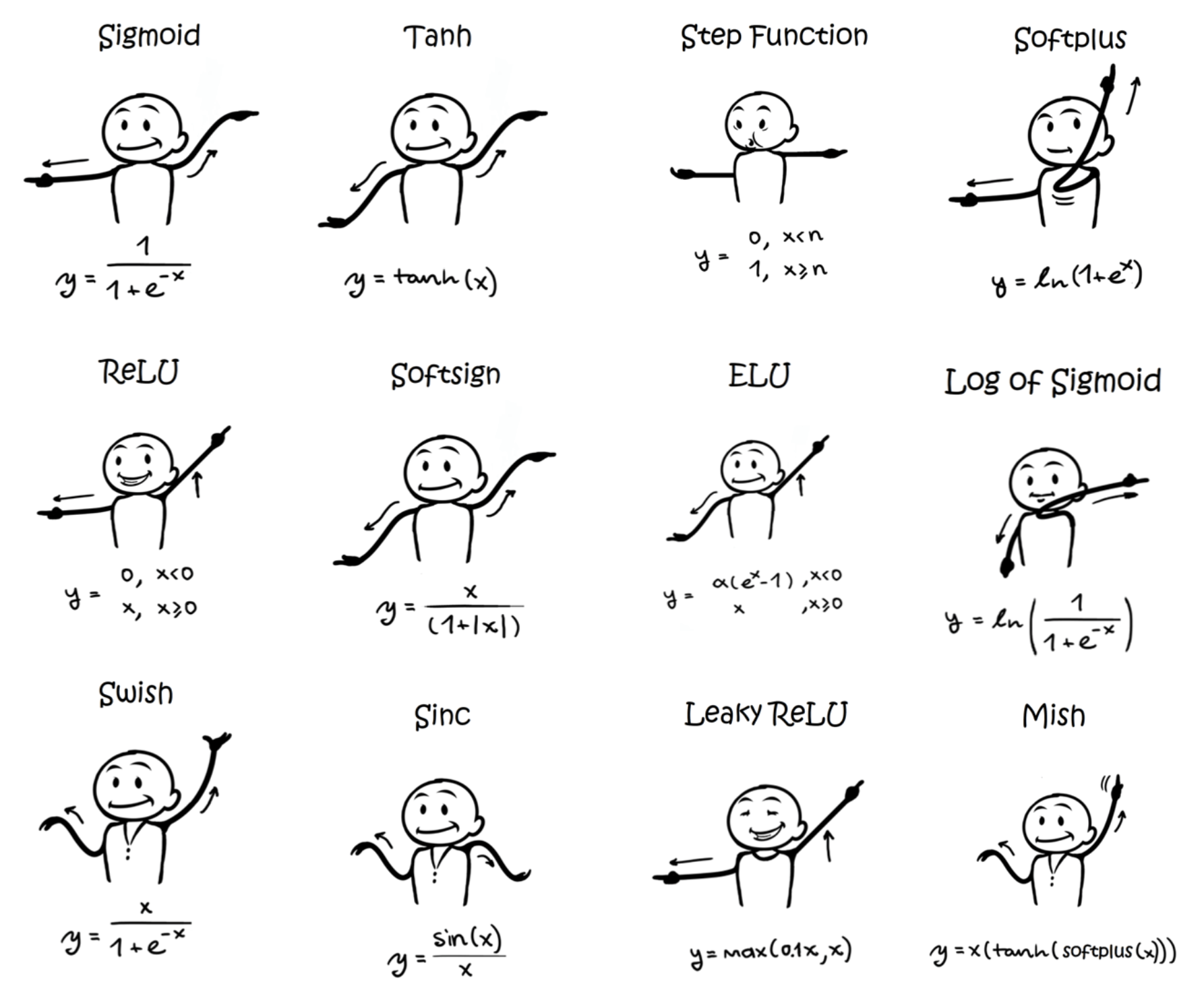
• hidden layer 를 설계할 때 위와 같이 선택할 수 있는 활성화 함수는 굉장히 다양하다.
  • 이 Wiki에는 한 눈에 표로 정리되어 있다.
• 활성화 함수는 크게 Sigmoid 계열과 구간 선형 함수로 정의되는 ReLU(Rectified Linear Unit) 계열로 구분할 수 있다.
  • Sigmoid 계열은 sigmoid, tanh(하이퍼볼릭 탄젠트) 등이 있으며, ReLU 계열은 ReLU, maxout, ELU 등이 포함된다.
  • ReLU 계열은 특정 구간에서 선형성을 갖고 있어서 연산 속도가 매우 빠르고 학습 과정을 안정적으로 만들어준다. 따라서 hidden layer 에서는 ReLU 계열을 활성화 함수로 사용하는 것이 좋다.
  • Sigmoid 계열은 연산 속도도 느리고 gradient vanishing 의 원인이 되어 neural network 학습에는 좋지 않지만, 값을 고정 범위로 만들어주는 기능이 있어 필요한 구조에서 다양하게 활용된다. 이러한 특징 때문에 output layer(출력층)에서 자주 사용될 수 있다.
• 위와 같이 다양한 activation function 이 연구되어 사용되고 있지만 아무렇게나 만드는게 아니라 몇가지 중요한 특징을 고려한다.
  • non-linearity in optimization landscape : non-linearity 를 추가한다.
  • not increase computational complexity of ML model : 연산의 부담이 증가하지 않아야 한다.
  • not hampler the gradient flow during training : 학습 과정에서 gradient 가 흐를 수 있도록 한다. 즉 미분 가능하여 gradient 가 구해지도록 한다.
  • retain the distribution of data : data 의 distribution 을 유지하도록 한다.
• 앞으로 위와 같은 특징들을 잘 염두하면서 특정 activation function 이 해당 특징들을 잘 지켜내고 있는지 살펴보자.
• 이 포스트에서는 먼저 Identity, Step Function, Sigmoid, Tanh, Softmax 를 정리한다.

Idenetity

• neural network 는 classification 과 regression 문제 모두에서 이용할 수 있다. 이 때 문제에 따라 출력층에서 사용하는 활성화 함수가 달라진다.

• regression 문제에서는 항등 함수(identity function)를 사용한다.

  \[f(x) = x\]

• 위 식에서 볼 수 있듯, 항등 함수는 입력을 그대로 출력한다. 출력층에서 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 되며, 항등 함수에 의한 변환은 화살표로 표시한다.

  

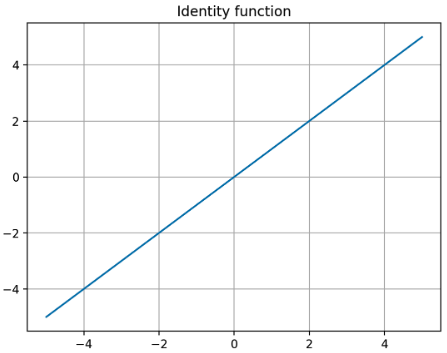
• 그러나 이는 우리가 위에서 살펴본 비선형 함수가 아니기 때문에 딥러닝에서 자주 사용하는 활성화 함수로 다뤄지지는 않는다.

Step Function

• 최초의 인공 신경망인 퍼셉트론에서 사용하던 활성화 함수다.

• 입력이 thresohold(default=0) 를 넘으면 1 을 출력하고, 그 외에는 0 을 출력하는 함수다.

  \[f(x) = \begin{cases} 0 & \text{if} \; x < 0 \\ 1 & \text{if} \; x \geq 0 \end{cases}\]

• 이를 그래프로 나타내면 다음과 같다.

  

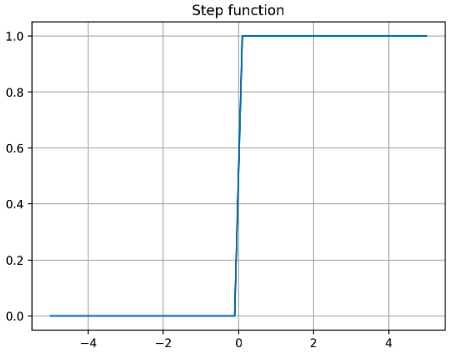
• 위 plot 에서 볼 수 있듯, step function 은 모든 구간에서 미분값이 0 이고 threshold 지점에서는 미분이 불가능하다.
• 따라서 gradient 를 이용하여 학습하는 역전파 알고리즘에 적용할 경우, 학습이 진행되지 않는다.
• 이로 인해 역전파 알고리즘에서 step function 을 대체할 미분 가능한 함수가 필요했고 그것이 Sigmoid 함수다.

Sigmoid

• Sigmoid 함수는 Step function 과 같이 범위가 $[0,1]$ 이면서 미분 가능하고 비선형 함수이다.

• Sigmoid 함수는 입력이 0 보다 클수록 1 에 가까운 숫자로 바꿔 주고, 반대로 0 보다 작을 수록 0 에 가까운 숫자로 바꿔 준다. 즉 0 ~ 1 까지의 값으로 바꿔주어 확률로 해석할 수 있게 해준다. 이 때문에 binary classification 의 경우 출력층에 사용된다.

  \[f(x) = \sigma(x) = \frac{1}{1 + e^{-x}}\]

• 또한 아래 plot 과 같이 매끄러운 곡성을 가지며 기울기가 급격하게 변하여 발생하는 gradient exploding 문제가 발생하지 않는다.

  

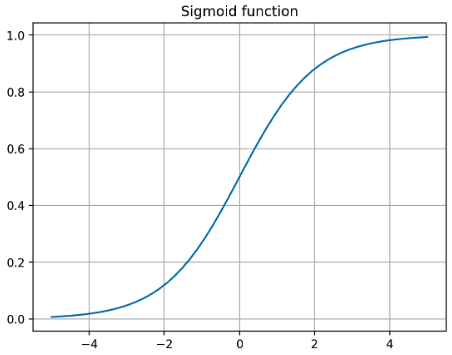
• 그러나 Sigmoid 함수에도 아래와 같은 단점들이 있다.

Saturation

• Sigmoid 함수는 입력값이 크거나 작을 때 기울기가 0 에 가까워지는 saturation 문제가 있다. 이는 기울기 소실(Gradient vanishing)을 야기하고 딥러닝 실무에서는 활성화 함수로 잘 사용하지 않는다.

• 이는 위 그래프와 함께 Sigmoid 함수의 도함수를 보면 알 수 있다. 자세한 미분 과정은 이 포스트에 정리했다.

  \[\sigma(x)' = \sigma(x)(1-\sigma(x))\]
• 역전파 과정에서 연쇄법칙에 따라 미분값이 곱해질 때, 0 에 가까운 값이 곱해지게 되면서 뒤로 갈수록 gradient 가 전달되지 않는다(사라지게 된다).
• 이에 따라 gradient vanishing 문제가 발생하고 neural network 의 학습이 잘 진행되지 않는다.

non-zero centered

• Sigmoid 함수는 zero centered 한 함수가 아니다. 즉 0 을 중심으로 하지 않고 0.5 를 중심으로 대칭된다. 이로 인해 Sigmoid 함수는 항상 양수를 출력한다.
• 따라서 가중치 업데이트 과정에서 앞쪽 layer 의 가중치가 뒤쪽 layer 에 전달될 때 항상 같은 방향으로 이동하게 된다.

• 아래와 같이 notation 이 정의되고 가중치 업데이트 과정이 나타난다고 해보자.

  \[\mathbf{h} = \mathbf{WX} + \mathbf{b}, \quad \mathbf{z} = \sigma(\mathbf{h}) \\ W \; \leftarrow \; W - \lambda \frac{\partial L}{\partial W} \\\]

• 가중치 업데이트에서 미분값은 아래와 같이 계산된다.

  \[\frac{\partial L}{\partial W} = \frac{\partial L}{\partial \mathbf{z}} \color{red}{\frac{\partial \mathbf{z}}{\partial \mathbf{h}}} \color{blue}{\frac{\partial \mathbf{h}}{\partial W}}\]
• 이 때 빨간색 term 은 sigmoid 의 미분이므로 항상 양수이다. 또한 파란색 term 은 계산결과가 $\mathbf{X}$ 이고 이는 앞 layer 에서 건너온 sigmoid 의 출력값이기 때문에 양수이다.
• 따라서 결과적으로 업데이트되는 값은 $\frac{\partial L}{\partial \mathbf{z}}$ 의 부호를 따라가게 되며, weight 업데이트는 + 또는 - 로 모두 같은 방향으로 업데이트가 일어나게 된다.
• 이러한 이유로 loss 가 최소가 되는 optimal weight 를 찾는 과정에서 zig-zag 형태로 업데이트가 일어나게 된다. 이렇게 되면 여러번 탐색을 해야 하기 때문에 비효율적이고 학습에 더 많은 시간이 들어가게 된다.
  • 단적인 예로 $w_1 = 0.5, w_2 = 0.5$ 이고 최적의 값이 각각 $0.4, 0.6$ 이라고 해보자.
  • 미분값이 항상 양수가 아니라면 각각 $-0.1, +0.1$ 로 한번에 찾아갈 수 있지만, non zero-centered 하여 항상 양수값만 가질 수 있다면 $+0.1, +0.2$ 이후에 $-0.2, -0.1$ 이렇게 불필요하게 2 번의 과정을 거쳐야 최적의 값으로 도달할 수 있다.

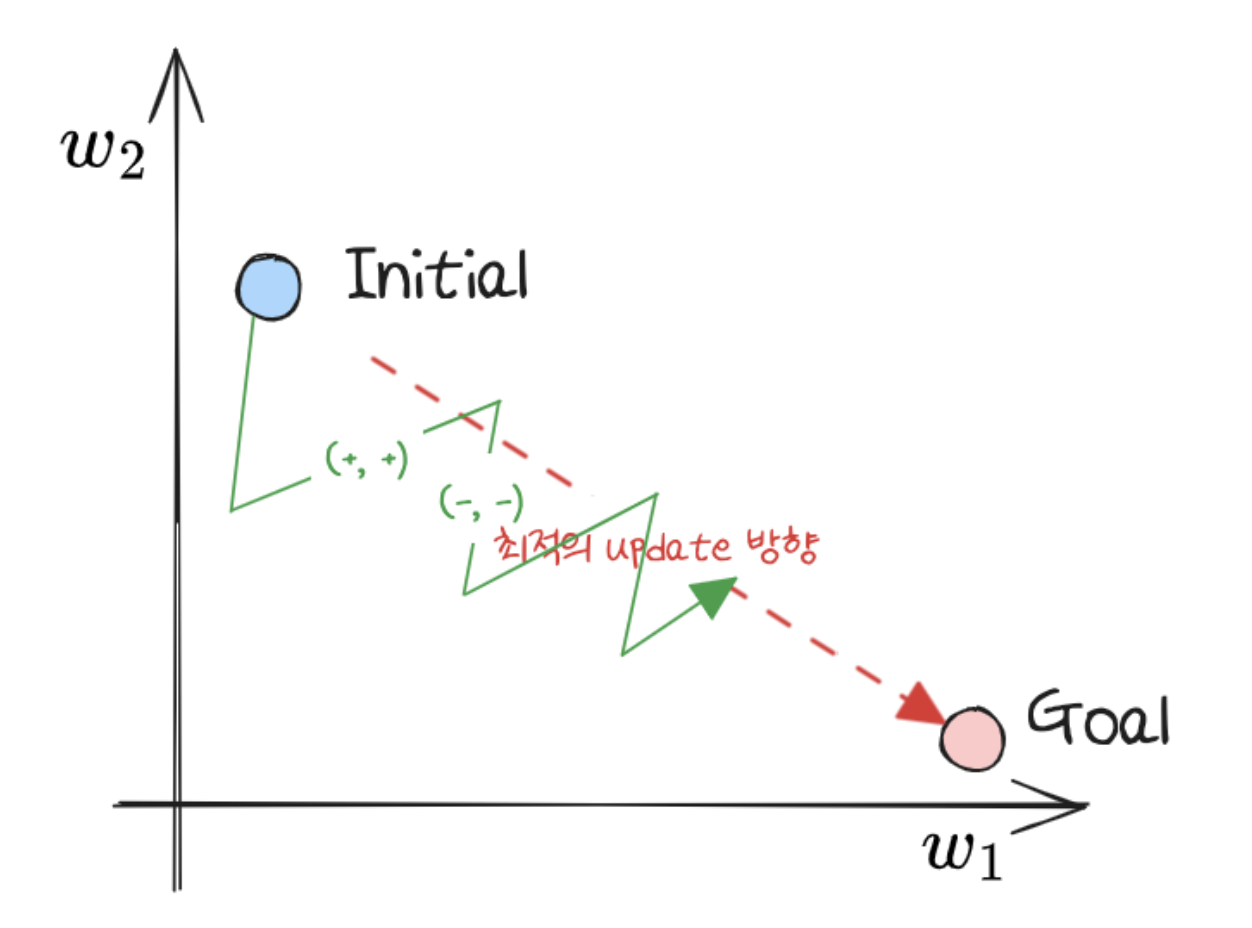  출처: https://devs0n.tistory.com/162

• 이처럼 활성화값(출력값)이 zero-centered 하지 않으면, parameter(weight, bias) 업데이트가 동일한 방향으로만 업데이트가 되어 학습 속도가 느려질 수 있다. 즉 convergence 에 방해가 된다.
• 또한 sigmoid 와 weight initailization 에서 정규분포로 가중치를 초기화하는 방식을 사용했을 때, 각 layer 에서 출력의 분산이 입력의 분산보다 더 크다.
• 이렇게 신경망이 위 layer 로 갈수록 분산이 계속 커져 가장 높은 층에서는 activation 값이 0 이나 1 로 수렴한다. 이는 Sigmoid 함수가 non-zero centered 라는 사실 때문에 더욱 그렇다.
• 또한 Sigmoid 함수는 항상 양수를 출력하므로 출력의 가중치 합이 입력보다 커질 가능성이 높다. 이를 bias shift(편향 이동) 라고 한다. 즉 layer 를 거칠수록 각 layer 에서 Sigmoid 에 대한 입력값이 0 에서 멀어지므로(계속 커지므로) gradient vanishing 현상이 나타날 수 있다.
• 이외에도 출력값이 너무 작아 학습이 잘 안되는 문제와 $\exp$ 연산으로 인해 비용이 크다.
• 이러한 단점들로 오늘날 Sigmoid 함수는 hidden layer 에서 활성화 함수로 잘 사용되지 않는다. 더 나아가 사용하지 말라고 하는 강의들도 있다.
• 그러나 0 에서 1 사이의 값으로 확률로 해석하여 binary classification 출력층에서 사용될 수 있다.

Tanh

• 위와 같은 Sigmoid 함수에서 non-zero centered 문제를 해결해줄 수 있는 활성화 함수는 Tanh 함수이다. 정확히는 Hyperbolic Tangent function 이라고 부른다.

• 즉 Sigmoid 함수의 한계를 보완하고 크기와 위치를 조정한 함수로 아래와 같은 식으로 나타낼 수 있다.

  \[\text{tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

• 아래 그래프와 같이 zero centered 하기 때문에, 최적화 시 zig-zag 형태의 업데이트나 bias shift 가 일어나지 않는다.

  

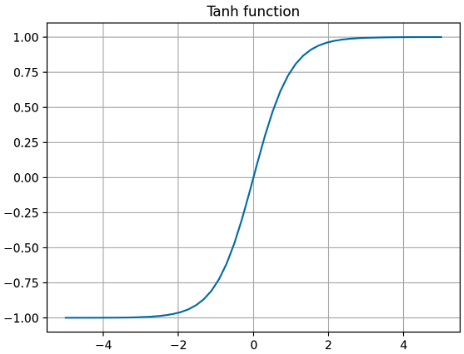
• 위 그래프에서 볼 수 있듯 값의 범위가 $[-1, 1]$ 로 activation 값이 양수, 음수 모두 나올 수 있기 때문에 Sigmoid 함수보다 학습 효율성이 좋다.
• 또한 Sigmoid 함수보다 범위가 넓기 때문에 출력값의 변화 폭이 더 크고, gradient vanishing 증상이 더 적다.
• 이러한 이유로 hidden layer 에서 활성화 함수로 sigmoid 를 쓴다면, 차라리 tanh 함수를 쓰는 것이 낫다. 그러나 큰 효과를 기대하기는 어렵다.

• 왜냐하면 tanh 함수는 sigmoid 함수를 transformation 하여 얻을 수 있는 것으로, 여전히 gradient 가 죽는 sautration 구간이 양수/음수 구간 모두 존재한다.

  \[\text{tanh}(x) = 2\sigma(2x) - 1\]
• 따라서 여전히 gradient vanishing 문제가 발생한다.

Softmax

• 세 개 이상으로 분류하는 multi classification 문제에서 output layer 에 사용되는 활성화 함수다.

• transformer 에서 attention 을 계산될 때 사용되긴 하지만 이는 activation 목적으로 사용되는 것이 아니고, hidden layer 에서는 잘 사용되지 않는다.

  \[f(x) = \frac{e^{x_i}}{\sum^J_{j=1} e^{x_j}} \quad i = 1, \ldots, J\]
• 위 식처럼 Softmax 함수의 출력은 모든 입력 신호로부터 영향을 받는다.
• 입력 받은 값을 출력으로 0 과 1 사이의 값으로 모두 정규화하며, 출력 값들의 총합은 항상 1 이 되는 특성을 가진 함수다. 이를 통해 Sigmoid 함수와 같이 확률로 해석할 수 있게 한다.
• 그러나 위와 같은 Softmax 의 식은 지수함수에 의해 numerical under-flow 와 over-flow 라는 치명적인 문제가 발생한다.
• 이에 관한 자세한 내용은 이 포스트에서 자세히 정리했다.

• 따라서 LogSumExp trick 을 사용하여 아래와 같은 식으로 구현한다.

  \[\hat y_j = \frac{\exp o_j}{\sum_k \exp o_k} = \frac{\exp(o_j - \bar{o}) \exp \bar{o}}{\sum_k \exp (o_k - \bar{o}) \exp \bar{o}} = \frac{\exp(o_j - \bar{o})}{\sum_k \exp (o_k - \bar{o})}\]
• 이러한 Softmax 함수는 Simgoid 함수의 multi class 버전이라고 생각할 수 있어, gradient vanishing 과 같은 문제가 그대로 나타날 수 있다. 따라서 hidden layer 가 아닌 output layer 에서 사용하는 것이 좋다.
• 한가지 기억하면 좋은 것이 지수함수는 단조 증가 함수(계속 증가하는 함수)이기 때문에, softmax 함수를 적용하더라도 각 원소의 대소 관계는 변하지 않는다는 것이다.
• 즉, 추론(inference) 단계에서 softmax 함수를 output layer 에 적용하지 않더라도 괜찮다는 의미다. 일반적으로 추론에서는 가장 큰 출력값에 해당하는 부류로 분류한다.
• 따라서 학습(train) 단계에서는 output layer 에서 softmax 함수를 이용하고, 추론 단계에서는 output layer 의 softmax 함수를 생략하기도 한다.
• 이 외에 softmax 에는 temperature 라는 계수가 등장한다. softmax 는 각 class 에 속할 확률을 구하는 것으로 $\text{softmax}(\mathbf{x})$ 가 분포를 의미한다고 할 수 있다.
• 이 때 경우에 따라서 하나의 인덱스에 집중된 날카로운 분포를 사용해야 되는 경우가 있고, 날카로움이 덜하고 평평한 느낌의 분포를 사용하는 것이 좋을 때가 있다.

• softmax 로부터 나오는 확률분포의 날카롭고 평평한 정도를 조절하기 위해서 temperature 를 사용한다. 이는 하이퍼파라미터로써, temperature $T$ 를 이용한 softmax 의 $i$ 번째 값은 아래와 같다.

  \[\text{softmax}_T(\mathbf{x})_i = \frac{\exp(x_i / T)}{\sum^d_{j=1} \exp(x_j / T)}\]

• $T$ 가 작을수록 날카로운 분포를 갖게 되고 $T$ 가 클수록 softmax 로 나온 분포가 평평해진다.

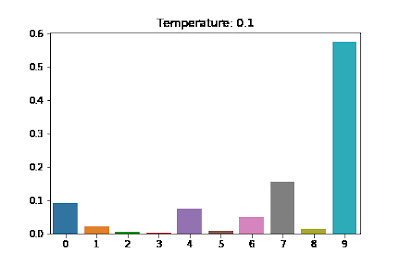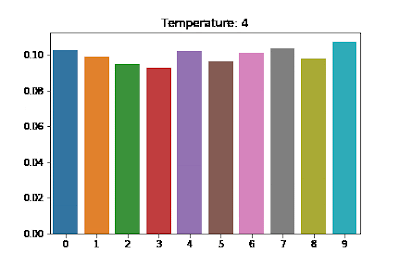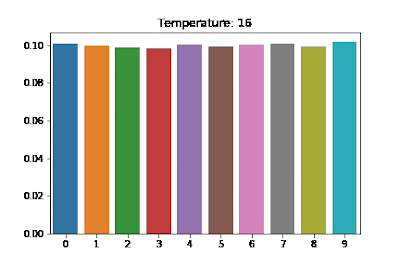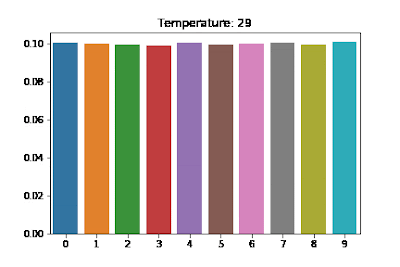  출처: https://medium.com/@harshit158/softmax-temperature-5492e4007f71

• 보통 큰 $T$ 에서 시작하면 경사하강법이 적절하게 동작하도록 할 수 있다. 즉 큰 temperature 계수에서는 각 클래스에 대해 확률 차이가 크지 않게 평평한 형태이고, 초반 학습 단계에서 경사하강법이 더 부드럽게 동작할 수 있다. 급격한 확률 변화 대신 각 클래스에 대해 좀 더 다양한 가능성을 두면서 학습을 진행할 수 있기 때문이다.
• 반면에 Attention mechanism 과 같은 harder decision 을 원한다면 $T$ 를 작게 하면 된다. 이를 통해 결정을 sharpen 하게 할 수 있다. 이러한 방법을 Annealing(담금질)이라고 하고, Self-attention mechanism 과 같은 MoE(Mixture of Experts) 에 유용하게 사용할 수 있다.
• 자세한 것은 transformer 카테고리에서 다룰 것이다.

Reference

• 이미지 출처: https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture05.pdf
• https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/

맨 위로 이동 ↑